Angles are everywhere. They define the corners of your home, the tilt of the Earth, and even the way your favorite movie scene is shot. While the Angle Converter tool makes switching between degrees, radians, and revolutions effortless, the concept of an angle is rich with history, utility, and universal meaning. From ancient Babylonian astronomers charting stars to modern-day engineers designing bridges, angles help us make sense of space and movement. They are fundamental to mathematics, physics, art, and even philosophy. In this article, we won’t just explain how to convert angles—we’ll explore why angles matter in science, culture, and everyday life. Whether you’re a student, researcher, or curious reader, this journey will reveal how something as simple as a turn or a corner can unlock the hidden geometry of the universe.
What Is an Angle?
An angle is more than just a pointy corner on a diagram—it's a fundamental concept in how we understand and describe the world around us. According to the National Institute of Standards and Technology (NIST), an angle is defined as “the figure formed by two rays sharing a common endpoint,” and it's measured by the amount of rotation one ray must undergo to align with the other.
In practical terms, angles are everywhere—from the way we tilt our heads to how we build bridges and rotate satellites. They help us interpret direction, orientation, and even balance. Without angles, geometry would collapse, engineering would be guesswork, and movement would be mathematically meaningless.
Angles come in a variety of forms:
%20(1).jpg)
Each type has real-world significance. Acute and right angles dominate everyday structures—walls, screens, and paper edges—while obtuse and reflex angles appear in design, architecture, and biomechanics. In physics, angular motion defines everything from planetary orbits to the spin of electrons. Even in perception, angles matter: our depth perception relies on the visual angles formed by our eyes.
Degrees, Radians, and Revolutions
Angles may seem simple at first glance, but their measurement has evolved through history, mathematics, and even culture. The three most common units—degrees, radians, and revolutions—form a universal system that allows us to describe rotation, orientation, and motion across disciplines.
The Core Relationship
The complete rotation of a circle is represented equivalently in three units:
|
Unit |
Value for 1 Full Circle |
Symbol |
|
Degrees |
360° |
° |
|
Radians |
2π |
rad |
|
Revolutions |
1 |
rev |
From this, we derive key conversions:
These equivalencies are not just for mathematicians—they power everything from digital animation to orbital calculations in spaceflight
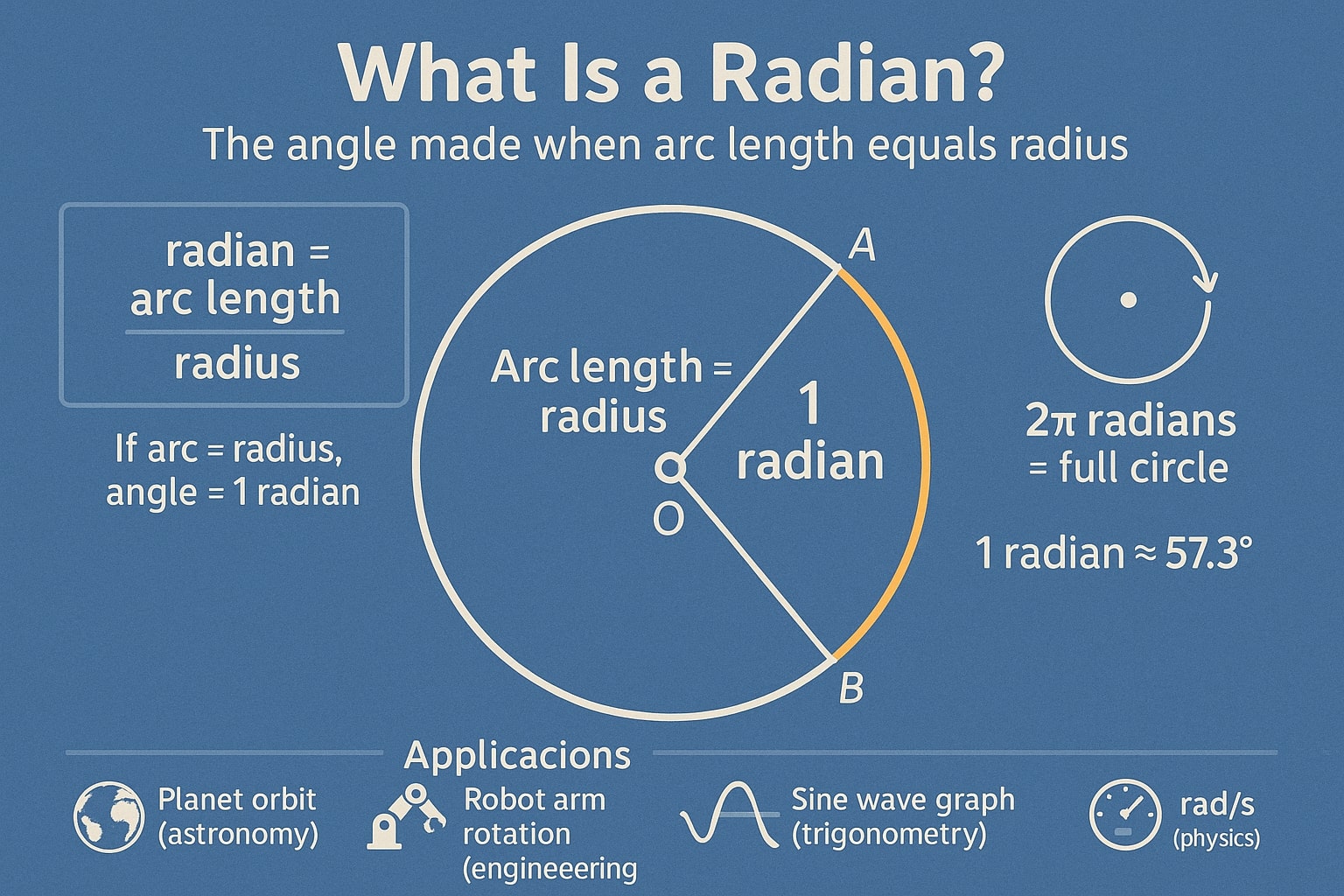
What Is a Radian?
A radian is the standard unit of angular measure used in advanced mathematics and physics. It's based on the radius of a circle. One radian is defined as the angle created when the arc length is equal to the radius of the circle.
Mathematically:
radian = arc length/radius
Since the circumference of a circle is 2πr, a full rotation around a circle equals 2π radians.
Thus:
Radians simplify many mathematical equations, especially in calculus, where trigonometric functions behave more cleanly and naturally when measured in radians.
Core Conversion Formulas
|
Conversion |
Formula |
|
Degrees → Radians |
rad = deg × (π / 180) |
|
Radians → Degrees |
deg = rad × (180 / π) |
|
Degrees → Revolutions |
rev = deg ÷ 360 |
|
Revolutions → Degrees |
deg = rev × 360 |
|
Radians → Revolutions |
rev = rad ÷ (2π) |
|
Revolutions → Radians |
rad = rev × 2π |
These formulas allow seamless conversion between systems whether you're programming, graphing functions, or interpreting scientific measurements.
Quick-Reference Table for Common Angles
|
Degrees (°) |
Radians (rad) |
Revolutions (rev) |
|
30° |
π/6 |
0.083 |
|
45° |
π/4 |
0.125 |
|
60° |
π/3 |
0.167 |
|
90° |
π/2 |
0.25 |
|
180° |
π |
0.5 |
|
270° |
3π/2 |
0.75 |
|
360° |
2π |
1.0 |
This table is particularly useful for students and professionals working with trigonometric functions, circular motion, or programming environments like JavaScript and Python.
Common Mistakes in Angle Conversion
-
Forgetting to switch calculator mode: Many students accidentally use degrees when radians are required (or vice versa), resulting in incorrect trigonometric outputs.
-
Miscalculating with π: Rounding π too early can lead to precision loss—especially in physics or engineering.
-
Mixing symbols and assumptions: Some scientific software assumes angles are in radians unless specified otherwise. Always double-check the expected unit.
Angle–Time Relationship in Real-World Systems
In a world increasingly governed by exactitude, from digital design to aerospace navigation, angles have become a crucial part of how we measure, model, and move through time. Every rotation, every trajectory, every structural alignment relies on precise angular measurement—often in real-time.
Whether you're a student solving for radians or an engineer adjusting satellite orientation, the Angle Converter plays a vital role. It doesn’t just save time—it respects time, ensuring seamless transitions between degrees, radians, and revolutions with no room for guesswork.
Analog Clock
-
1 full rotation = 360°
-
1 hour = 60°
-
1 minute = 6°
→ Angle per minute=360/60= 6°
Angular Velocity in Robotics / Physics
-
Standard angular unit for measuring rotation speed: radian/second (rad/s)
-
If an object rotates θ radians in t seconds:
→
where ω is an angular velocity
Revolutions and Time-Based Rotation
-
1 revolution = 360° = 2π radians
-
Time per rotation:
→ Time per rev=1/Revolutions per second
Euclid – The Father of Angles
Long before calculators or angle converters existed, one man helped shape the way we understand space itself: Euclid of Alexandria, often called the “Father of Geometry.” Living around 300 BCE, Euclid’s seminal work Elements, laid the foundation for modern geometry—and with it, our concept of angles.
In Elements, Euclid didn’t just define the angle; he systematized it. He described a right angle as the result when a straight line standing on another makes the adjacent angles equal—a moment of balance and symmetry that would guide architects and scientists for millennia.
Euclid’s rigorous approach helped distinguish angles not just by measurement, but by relationship. His principles continue to shape architecture, astronomy, and even computer graphics. Without Euclid, a 90° angle might never have become “right”—not just in value, but in name.
%20(1).jpg)
To explore more tools like this one, visit the Conversion category—your gateway to smarter, faster, and more accurate calculations across physics, math, and real-world scenarios.

