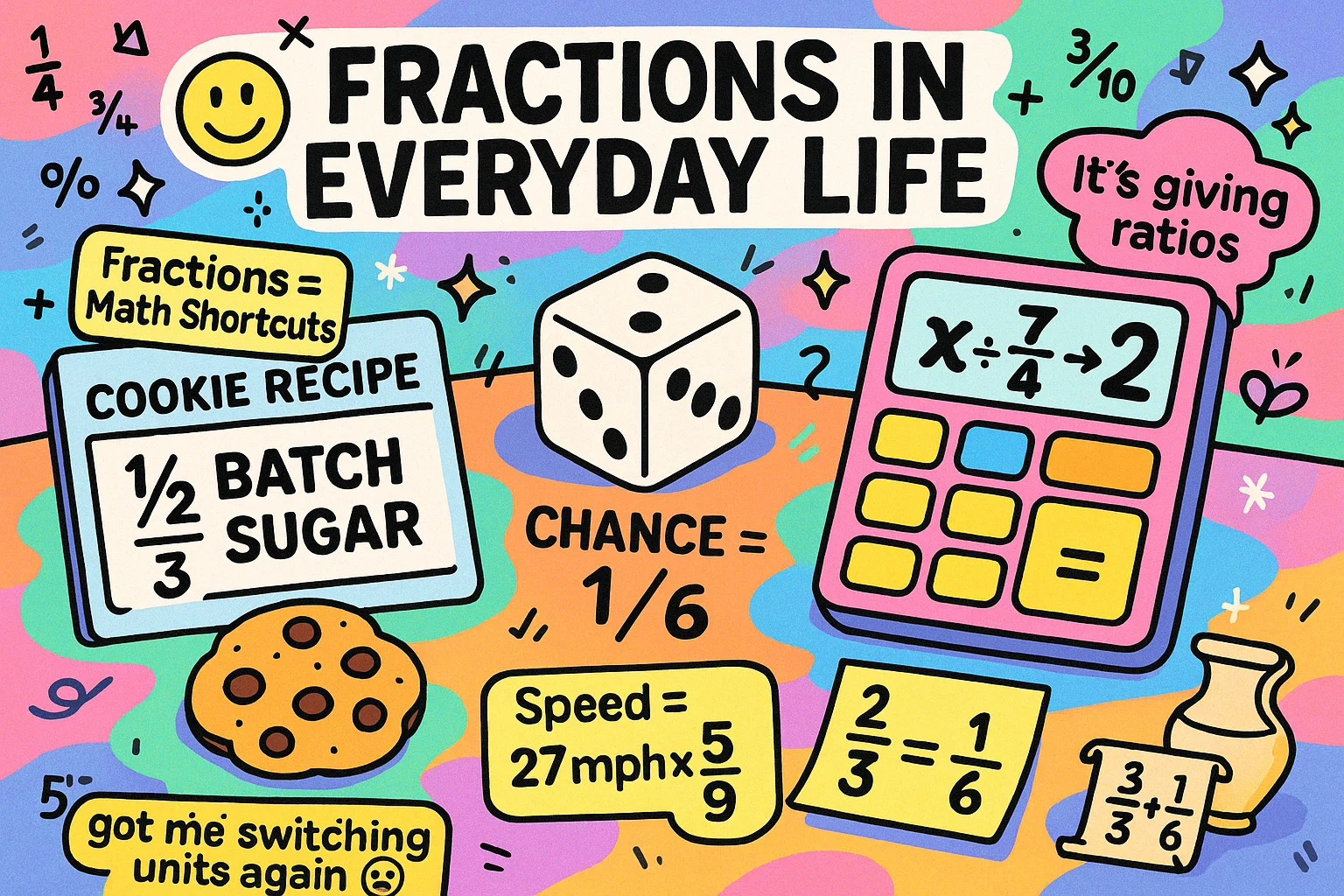Fraction Basic Calculator

Fractions show up in everything—recipes, construction, taxes, even when sharing a pizza. Getting good at fraction calculation can save time, prevent mistakes, and build confidence for students and professionals alike. From adding ⅔ + ¼ to multiplying ⅝ × ¾, this guide breaks down the steps, clears up common confusion, and shows how fractions connect to real-life problems.

What Is a Fraction?

A fraction is a way to show a part of a whole. It’s written with two numbers stacked, separated by a line — the top number is the numerator (the part you have), and the bottom is the denominator (the total parts that make up the whole).

Think of a pizza: if it’s cut into 8 equal slices and you eat 3, you’ve eaten 3⁄8 of the pizza. The 3 shows your slices, and the 8 shows the whole pizza.

Fractions show up all the time, not just in math class. Recipes often call for ½ a cup of sugar or ¾ teaspoon of salt. Construction and measuring use them constantly — like a board that’s 5⁄8 inch thick. They even pop up when splitting a bill among friends or figuring out a discount.

Examples you see every day:

• Half a pie: ½

• Three quarters of a tank of gas: ¾

• Five-eighths inch on a ruler: 5⁄8

Fractions keep numbers flexible — they help describe things that don’t fit neatly into whole numbers.

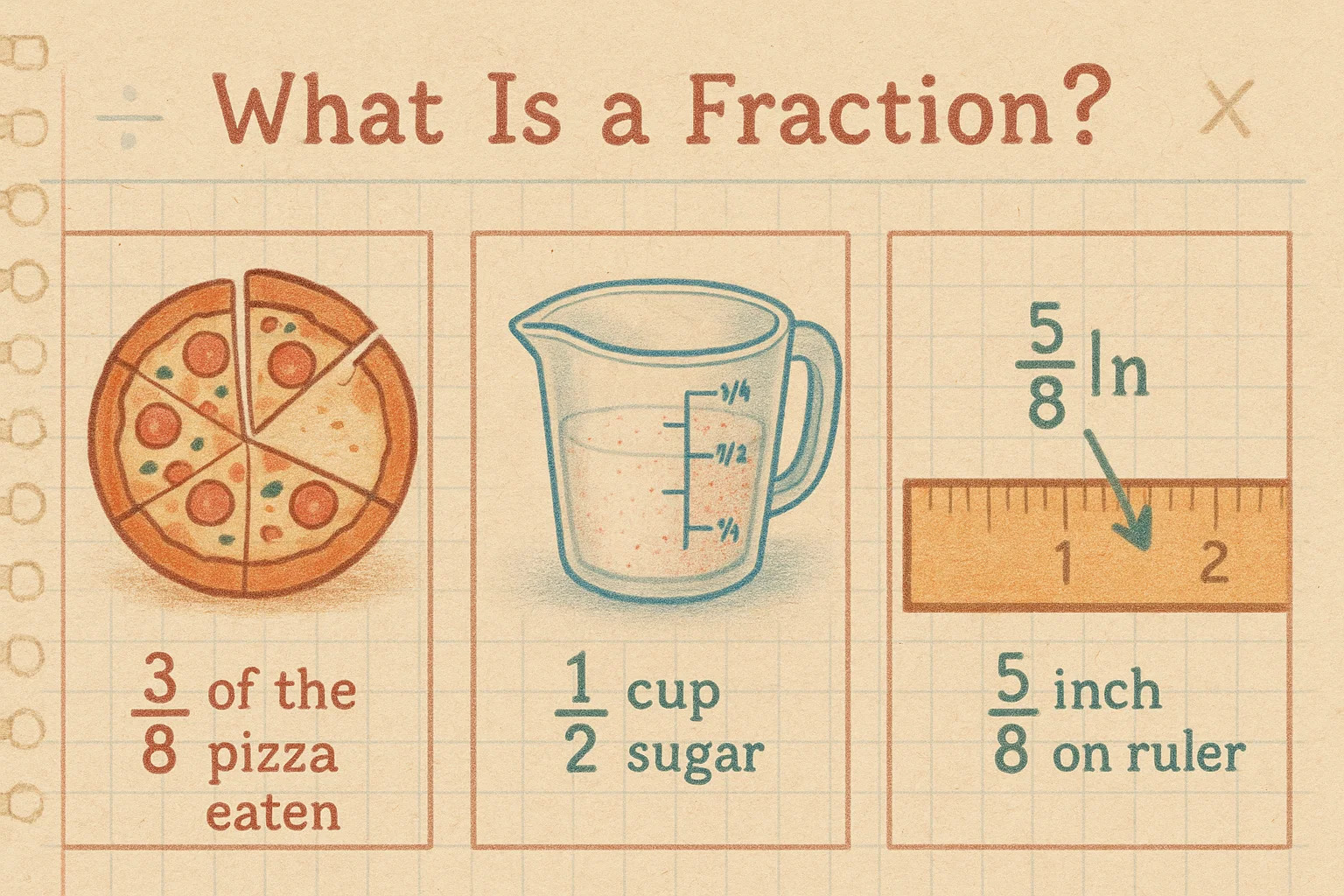
Adding Fractions

Adding fractions is easy when both fractions already share the same denominator — just add the numerators and keep the denominator the same.

For example: 1⁄4 + 2⁄4 = 3⁄4

But when the denominators are different, you need to make them match first. The easiest way is to find a common denominator — usually the least common multiple (LCM) of the two denominators. Then, adjust the fractions so they share that denominator before adding.

Example with different denominators: 1⁄3 + 1⁄6

• The least common denominator is 6.

• Rewrite 1⁄3 as 2⁄6.

• Now add: 2⁄6 + 1⁄6 = 3⁄6.

• Simplify by dividing numerator and denominator by 3: 3⁄6 = ½.

A quick trick: if one denominator is a multiple of the other (like 2 and 4), you can skip finding the full LCM and just use the larger denominator.

Subtracting Fractions

Subtracting fractions follows almost the same steps as adding — but with a minus sign instead of a plus.

If the fractions share the same denominator, just subtract the numerators and keep the denominator the same:

5⁄8 − 3⁄8 = 2⁄8, which simplifies to 1⁄4.

When the denominators are different, you’ll need to find a common denominator first (usually the least common multiple). Then, rewrite each fraction so they share the denominator and subtract:

Example with different denominators:
5⁄6 − 1⁄3

• The least common denominator is 6.

• Rewrite 1⁄3 as 2⁄6.

• Now subtract: 5⁄6 − 2⁄6 = 3⁄6.

• Simplify: 3⁄6 = ½.

If the numerator of the smaller fraction is larger after adjusting, the result can be negative. For example:
1⁄4 − 3⁄4 = −2⁄4 = −½.

Quick note: You can also rewrite negative answers as mixed numbers if needed, but leaving them as improper fractions (−5⁄4) is perfectly fine in most math problems.

Multiplying Fractions

Multiplying fractions is often the simplest operation — no need for a common denominator. The rule is straightforward: multiply the numerators together, multiply the denominators together, then simplify the result if possible.

Here’s how it looks step by step:

Example: 2⁄3 × 3⁄5

1. Multiply the numerators: 2 × 3 = 6.

2. Multiply the denominators: 3 × 5 = 15.

3. Combine: 6⁄15.

4. Simplify by dividing both by 3: 6⁄15 = 2⁄5.

This works the same whether the fractions are proper (1⁄2) or improper (7⁄4).

Another example with larger numbers: 5⁄8 × 4⁄10

1. Numerators: 5 × 4 = 20.

2. Denominators: 8 × 10 = 80.

3. Combined fraction: 20⁄80.

4. Simplify: divide both by 20, and you get 1⁄4.

One useful shortcut is cross-canceling before multiplying. If a numerator and a denominator share a factor, you can reduce them first to keep numbers smaller: 6⁄10 × 5⁄9

• Before multiplying, notice 10 and 5 share a factor.

• Simplify 5⁄10 into 1⁄2.

• Now the problem is 6⁄2 × 1⁄9 = 3 × 1⁄9 = 3⁄9 = 1⁄3.

Did you know?
Multiplying by a fraction smaller than 1 always makes the result smaller. For example, ¾ × ½ = ⅜, which is less than both starting fractions.

Dividing Fractions

Dividing fractions may feel tricky at first, but it’s really just one extra step beyond multiplying. Instead of dividing directly, you flip the second fraction (find its reciprocal) and then multiply as usual.

This “flip and multiply” rule is a shortcut that works every time because dividing by a fraction is the same as multiplying by its inverse.

Example: ¾ ÷ ½

1. Keep the first fraction as it is: ¾.

2. Flip the second fraction (½ becomes ²⁄₁).

3. Multiply: ¾ × ²⁄₁ = ⁶⁄₄.

4. Simplify: divide numerator and denominator by 2 to get ³⁄₂.

5. Optional: rewrite as a mixed number: 1½.

Another example: ⁵⁄₆ ÷ ¹⁰⁄₉

1. Flip ¹⁰⁄₉ to get ⁹⁄₁₀.

2. Multiply: ⁵⁄₆ × ⁹⁄₁₀ = ⁴⁵⁄₆₀.

3. Simplify: divide both by 15, giving ¾.

A quick check: dividing by a fraction less than 1 usually makes the answer bigger, while dividing by a fraction greater than 1 makes it smaller.

Real-world tie-in: If a recipe calls for ¾ of a cup but you only want half the recipe, you’re effectively doing ¾ ÷ 2. Using the rule, that’s ¾ × ½ = 3⁄8 of a cup.

Fact to remember: You never divide fractions by finding a common denominator. Always flip the second one and multiply — it’s faster and avoids mistakes.

How Fraction Operations Connect to Bigger Math Ideas

Fractions might seem like just another thing you learned in school, but they actually pop up everywhere once you start looking — and not just on a math test. Whenever you add, subtract, multiply, or divide fractions, you’re using ideas that tie into everyday life and even more advanced math without realizing it.

Think about it:

• Ratios and recipes: When you reduce ⁸⁄₁₂ down to ²⁄₃, you’re not just simplifying — you’re describing a ratio. That same ratio could help you double a cookie recipe or adjust ingredients when you only want half a batch.

• Algebra without the scary name: Solving something like x ÷ ¾ = 2 is really just the same trick you already know — flip ¾ to ⁴⁄₃ and multiply. It’s fractions doing the heavy lifting behind what looks like an equation.

• Unit conversions you actually use: Ever switched between Fahrenheit and Celsius? The formula uses the fraction ⁵⁄₉. Or maybe you’ve had to convert miles per hour to meters per second — fractions make that possible.

• Chance and probability: Rolling a six-sided die? Your chance of getting a 4 is ¹⁄₆. Figuring out the odds of two events happening often means adding or multiplying fractions, even if you don’t notice it.

Fractions are more than numbers with lines in the middle — they’re tools that make sense of how things relate, scale, and change. Once you see how often they show up, they start feeling less like homework and more like shortcuts you already know how to use.

Fun fact: The ancient Egyptians wrote almost every fraction using only 1 in the numerator. To write something like ²⁄₃, they’d break it into ½ + ¹⁄₆. It worked, but our modern fractions are definitely easier on the eyes.