Mixed numbers — think 2 ½ or 5 ¾ — are more than just school-time math problems. They’re how recipes are written, how lumber is sold, and even how distances in sports are measured.
Mixed Numbers vs. Improper Fractions
If you've ever measured out 2 ½ cups of flour or heard someone say they ran 5 ¾ miles, you've already worked with mixed numbers. A mixed number is a whole number combined with a proper fraction — like 3 ½, which is really just three wholes and a half more. They're practical, familiar, and used in everyday life far more often than we realize.
On the flip side, improper fractions look a little messier but follow the same math. These are fractions where the numerator (the top number) is equal to or greater than the denominator (the bottom number) — for example, ⁷⁄₂. That’s the same value as 3 ½, just written differently.
So why do we use two forms for the same thing? Mixed numbers are easier for people to interpret at a glance, while improper fractions are easier for actual calculations, especially in algebra or programming logic.
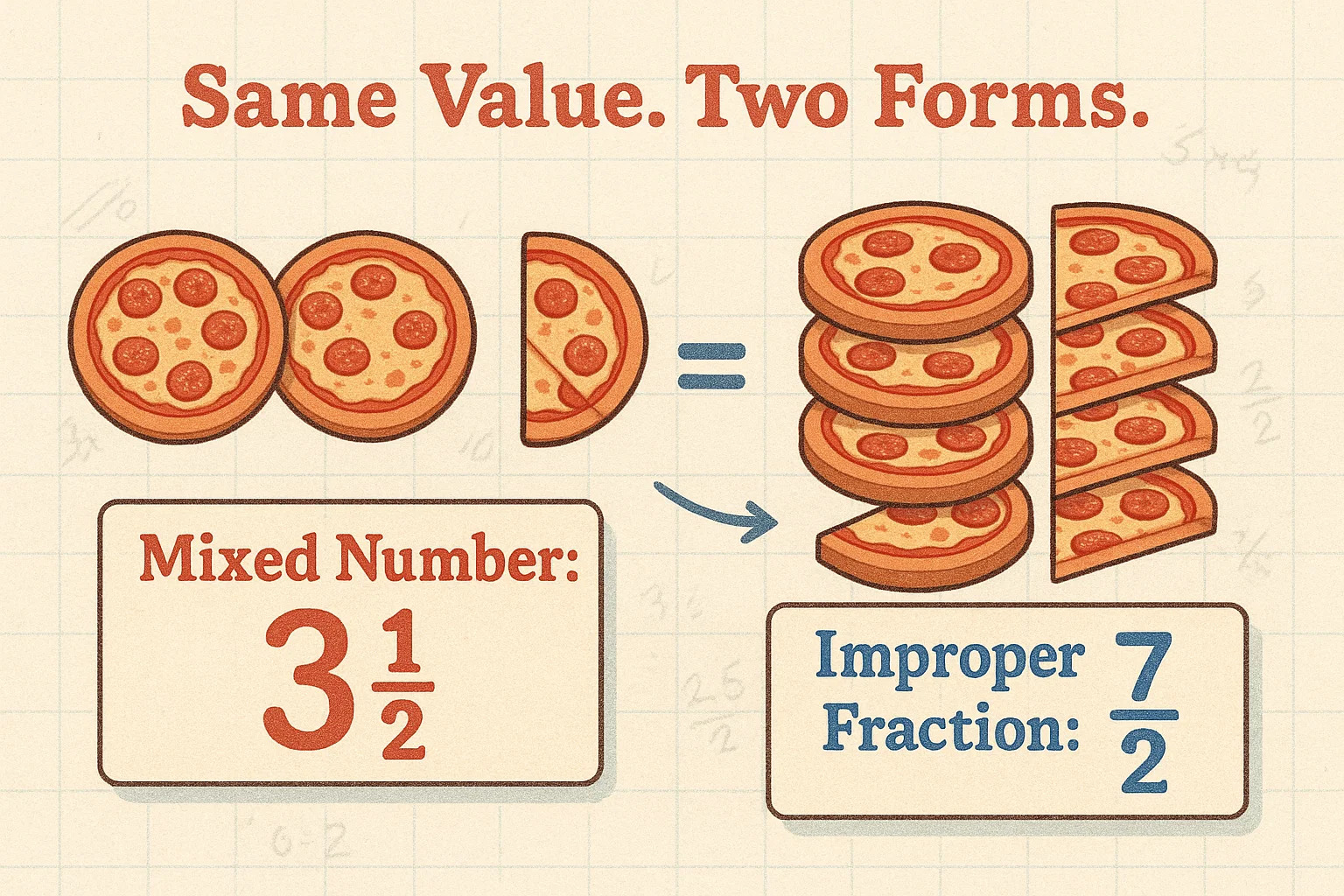
How to convert a mixed number to an improper fraction:
Say you have 4 ⅗.
-
Multiply the whole number by the denominator: 4 × 5 = 20
-
Add the numerator: 20 + 3 = 23
-
Place over the original denominator: ²³⁄₅
So 4 ⅗ becomes ²³⁄₅.
That’s a common process when you're trying to convert mixed number to improper fraction before multiplying or dividing them.
How to convert an improper fraction back to a mixed number:
Take ¹¹⁄₄.
-
Divide numerator by denominator: 11 ÷ 4 = 2 R3
-
The quotient is your whole number (2), and the remainder (3) is your new numerator
-
Keep the original denominator: 2 ¾
That’s the way to simplify a mixed number if you're starting from an improper format.
Fun Fact: “During the Apollo 13 mission, NASA engineers used slide rules and hand-calculations involving fractions like 2 ⁵⁄₈ to quickly reroute the spacecraft and save the crew.” — NASA archives¹
How Fraction Mixed Numbers is Calculated
When it comes to adding, subtracting, multiplying, or dividing mixed numbers, there’s a bit of a dance between whole numbers and fractions. The secret? Keep the math simple, clean — and always, always simplify when you're done. Whether you're doubling a recipe or solving a test problem, these quick rules will help you move fast and stay accurate.
Add and Subtract
Start by separating the whole number and fractional part. Mixed numbers have both, so work with each part on its own first, then bring them back together at the end.
Let’s walk through an example:
Add: 2 ½ + 3 ¾
-
Add whole numbers: 2 + 3 = 5
-
Add fractions: ½ + ¾ → Convert to common denominator → ²⁄₄ + ³⁄₄ = ⁵⁄₄
-
Now you’ve got: 5 + ⁵⁄₄ → But ⁵⁄₄ = 1 ¼, so final answer:
→ 6 ¼
Subtract: 5 ⅚ − 2 ⅔
-
Whole numbers: 5 - 2 = 3
-
Fractions: ⁵⁄₆ − ²⁄₃ → Convert ²⁄₃ = ⁴⁄₆ → ⁵⁄₆ − ⁴⁄₆ = ¹⁄₆
-
Final answer: 3 ¹⁄₆
When subtracting results in a negative fraction (e.g., ¼ − ¾), you may need to borrow from the whole number. Don’t skip this step — it’s where most errors creep in. When subtracting results in a negative fraction (e.g., ¼ − ¾), you may need to borrow from the whole number — or double-check your simplified answer using the Fraction Simplifier.
Multiply
Multiplying mixed numbers always starts with conversion.
Let’s say you're working with: Multiply: 2 ⅓ × 1 ½
-
Convert both to improper fractions:
2 ⅓ = ⁷⁄₃
1 ½ = ³⁄₂ -
Multiply across:
⁷⁄₃ × ³⁄₂ = ²¹⁄₆ -
Simplify:
²¹⁄₆ = 3 ½
Now you’re cooking.
Fact Block: “A Chicago high school study found students who practiced converting mixed numbers before multiplying improved test scores by 27% compared to those who guessed based on visuals.” — U.S. Department of Education study²
Multiplying works cleanly because you're working with all numbers — no need for a common denominator like in addition or subtraction. Not sure if your multiplication is correct? Try solving it first on paper, then run the result through a Fraction Calculator to compare.
Division
Division gets a bad reputation, but it’s just multiplication in disguise — literally.
Let’s try: Divide: 3 ¾ ÷ 1 ½
-
Convert to improper fractions:
3 ¾ = ¹⁵⁄₄
1 ½ = ³⁄₂ -
Flip the second fraction (the divisor):
³⁄₂ becomes ²⁄₃ -
Multiply:
¹⁵⁄₄ × ²⁄₃ = ³⁰⁄₁₂ -
Simplify:
³⁰⁄₁₂ = 2 ½
That’s it — flip and multiply.
If your answer is in an improper form like ²¹⁄₄, you can leave it that way for algebra or formal writing, or turn it into a mixed number (5 ¼) for day-to-day uses.
Whether in the classroom or the kitchen, knowing how to break down these calculations gives you the power to handle any math — no matter how mixed up the numbers look. If your answer is in an improper form like ²¹⁄₄, you can leave it that way for algebra or formal writing, or turn it into a mixed number (5 ¼) for day-to-day uses — or even double-check your steps using the Math Calculator.
When a Fraction Saved the Job Site
It’s not just classrooms where mixed numbers matter — sometimes they save time, money, and entire projects.
A construction foreman in Des Moines, Iowa, once shared how a single misread measurement almost derailed a school renovation job. The blueprint specified 8 ⅜ inches for the custom metal trim. A new apprentice, unfamiliar with fractional conversions, read it as 8.3 inches instead. The result? A batch of aluminum panels that were too short — by nearly ¹⁄₁₆ inch, just enough to fail inspection.
The mistake cost the team a full week of rework and over $4,000 in materials.
“I learned the hard way — decimals aren’t always your friend. Mixed numbers are what real-world tape measures use. It’s ⅜, not 0.375, and that difference can cost your paycheck.” — Tim Vega, construction lead, Vega & Sons Build Co.⁴
Now, before any measurements are sent to the fabrication shop, the crew double-checks with a printed fraction-to-decimal chart taped to every toolbox — and new hires get a quick lesson in adding and subtracting mixed numbers using common denominators.
Mixed numbers aren’t just academic fluff. They show up in blueprints, recipes, invoices, sports stats, and even tool calibration. Getting comfortable with how they work isn’t about passing a quiz — it’s about moving confidently through the real world, tape measure in hand.

- NASA. “Apollo 13 Timeline.”
-
U.S. Department of Education. “High School Math Study.”
-
Napa Valley College Baking & Culinary Program, anecdotal interviews, March 2023
-
Interview with Tim Vega, June 2022. Building Standards & Inspection, Iowa Department of Public Safety

