What a Right Triangle Is
A right triangle is any triangle with one angle measuring exactly 90°. That single right angle creates two sides, called legs, that meet at the corner, and one longer side opposite the angle, called the hypotenuse. In most formulas, the legs are labeled a and b, and the hypotenuse is c.
Right triangles pop up almost everywhere — from the slope of a roof to the support beams in a bridge, or even the shadow cast by a streetlamp. In math, they’re a favorite because they make it easy to work out missing sides or angles with just a few numbers.
What makes them stand out is their built‑in relationship between the three sides. Thanks to the Pythagorean theorem, if you know any two sides, you can always find the third. That’s why right triangles are the foundation for everything from basic geometry to trigonometry and physics.

How to calculate right triangle?
Every right triangle follows one simple rule: a² + b² = c²
This is the Pythagorean theorem, and it links the two legs (a and b) with the hypotenuse (c). If you know any two of these sides, you can always solve for the third.
For example, if the legs are 3 and 4 units long, the hypotenuse is:
c = √(3² + 4²) = √(9 + 16) = 5
This 3–4–5 triangle is a classic example because the numbers are clean, but the same rule works for any right triangle — even ones with decimals or big values.
You can also rearrange the formula to find a missing leg:
-
a = √(c² − b²) -
b = √(c² − a²)
These quick versions keep calculations simple whether you’re working by hand or double-checking your results.
Finding Angles in a Right Triangle
Once the sides of a right triangle are known, figuring out the angles is straightforward with a bit of trigonometry. The most common shortcuts come from the triangle’s natural ratios:
-
Using tangent:
θ = arctan(a⁄b)— perfect when you know both legs. -
Using sine:
θ = arcsin(a⁄c)— useful when a leg and the hypotenuse are known.
These functions make it simple to uncover the missing angles. Once you have one acute angle, the other is just 90° − θ.
For anyone double-checking or exploring more, you can try related tools like the Trigonometry Calculator to make these angle checks fast.
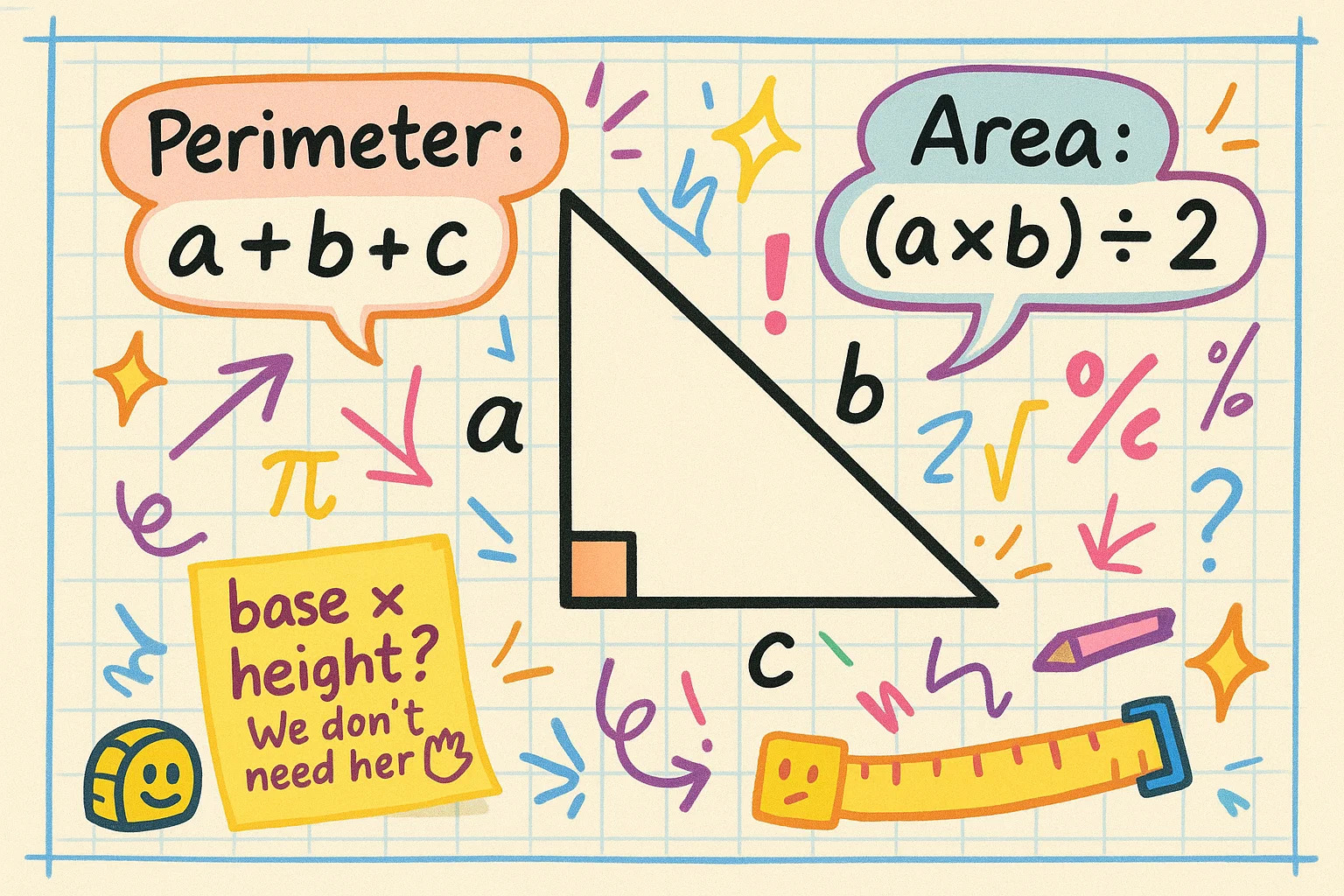
Perimeter and Area of a Right Triangle
Once you’ve found the sides of your right triangle, calculating its perimeter and area is straightforward. The perimeter is simply the sum of all three sides: P = a + b + c
For the area, there’s a shortcut that works for every right triangle: A = (a × b) ÷ 2
Because the two legs form a perfect right angle, they act as the base and height, so you don’t need any extra formulas or altitude lines.
For example, if a triangle has legs of 6 and 8 units, the hypotenuse c is 10 (by the Pythagorean theorem). The perimeter is 6 + 8 + 10 = 24, and the area is (6 × 8) ÷ 2 = 24.
These formulas make it easy to quickly size up a triangle whether you’re working on homework, construction plans, or even mapping out a DIY project.
Common Right Triangle Ratios
Some right triangles show up so often in math and real life that they’re worth memorizing. These “special triangles” have fixed side ratios, which means you can skip extra calculations and find missing sides or angles almost instantly.
The two most common are:
-
30°–60°–90°triangle
-
The sides always follow the ratio
1 : √3 : 2. -
The shortest side (opposite 30°) is your reference — double it for the hypotenuse, and multiply by √3 for the longer leg.
45°–45°–90° triangle
-
Both legs are the same, and the hypotenuse is always leg × √2.
-
The ratio is
1 : 1 : √2.
Quick reference table:
|
Triangle Type |
Leg : Leg : Hypotenuse |
|
30°–60°–90° |
1 : √3 : 2 |
|
45°–45°–90° |
1 : 1 : √2 |
Spotting these patterns can save time, especially in geometry or trigonometry problems.
Want to practice more triangle problems? Check out our Math Calculator, Pythagorean Theorem Calculator, and Trigonometry Calculator.

