Ellipsoid Volume Calculator

Let’s face it—"ellipsoid" isn’t exactly part of our everyday vocabulary. But surprisingly, ellipsoids are all around us. Ever cradled an egg, tossed a rugby ball, or seen Earth from space? You’ve encountered one. For all types of 3D shapes—from cones to pyramids—you’ll find everything under the main Volume Calculator page.

What Exactly Is an Ellipsoid?

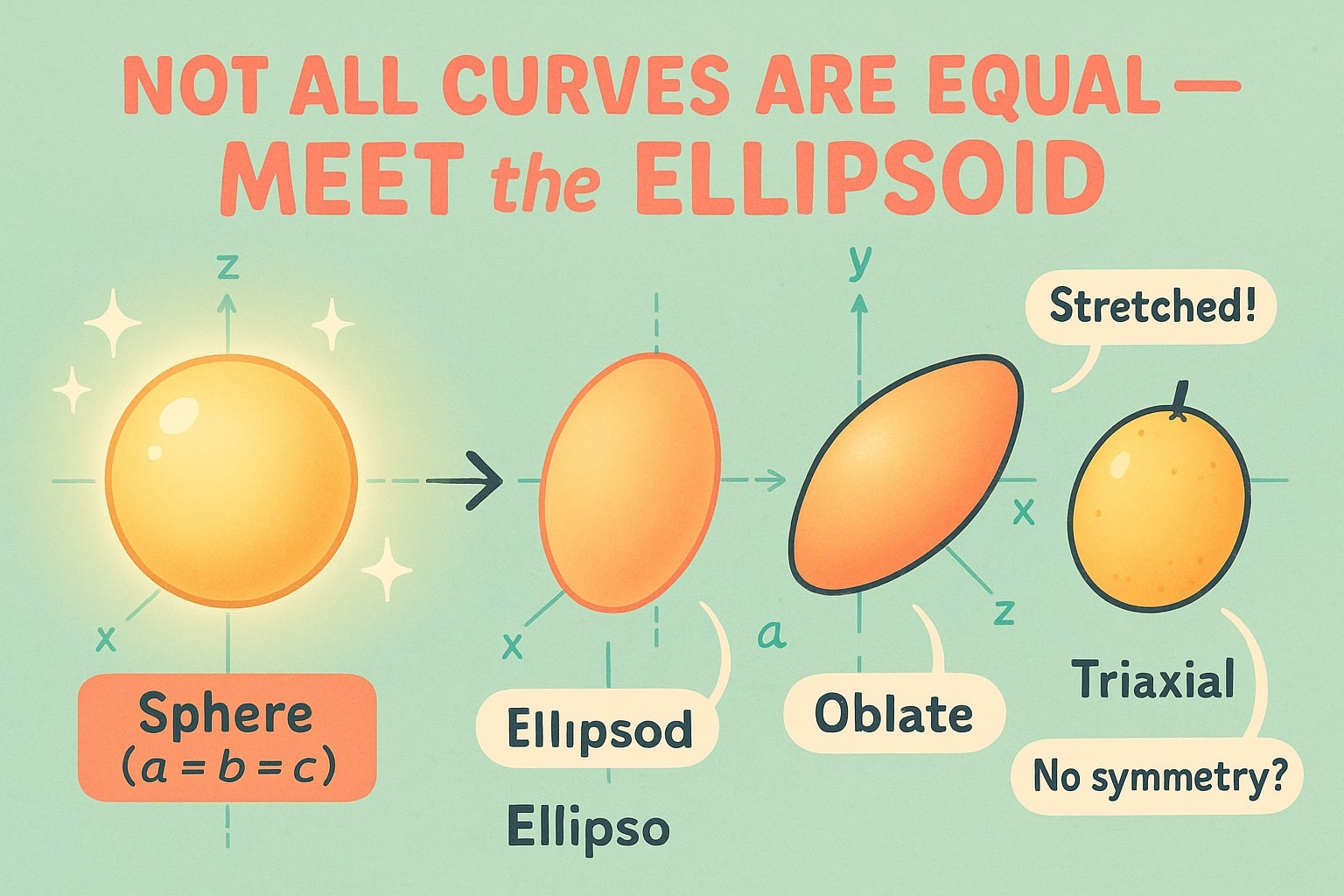
Start with a sphere—a perfect 3D round object. Now picture gently flattening it or pulling it out sideways. That smooth, rounded shape that’s not quite equal in every direction? That’s an ellipsoid.

In geometric terms, an ellipsoid is described using three axes:

• a = length along the x-axis

• b = length along the y-axis

• c = length along the z-axis

If a, b, and c are all equal, congrats—you’re looking at a sphere. But when they differ, you're in ellipsoid territory.

There are a few common types:

• Prolate ellipsoids: stretched along one axis (like a rugby ball)

• Oblate ellipsoids: squished along one axis (like Earth!)

• Triaxial ellipsoids: all three axes are different (no symmetry—think of oddly shaped fruits or medicine capsules)

From the shape of planets to cells and even fish eggs, ellipsoids show up more than you’d imagine. That’s why knowing how to calculate their volume actually comes in handy.

Once you’ve calculated the volume, you can quickly convert it into liters, gallons, or other units using the Volume Converter.

How to Calculate Ellipsoid Volume

Here's the good news: the volume formula is refreshingly simple. If you know the three semi-axis lengths (a, b, and c), just plug them into this:

Volume = (4/3) × π × a × b × c

That’s it. You multiply the three semi-axes together, then multiply by pi (π), then by four-thirds.

Quick Note: Make sure you're using the semi-axes, not the full diameters. If your ellipsoid is 10 cm wide, you should use 5 cm for that axis in the formula.

Let’s say your ellipsoid has semi-axes of 4 cm, 3 cm, and 2 cm.
You’d calculate the volume like this:

Volume = (4/3) × π × 4 × 3 × 2 = (4/3) × π × 24 ≈ 100.53 cm³

Now, if all three semi-axes are equal—say, 5 cm each—your ellipsoid is actually a sphere. In that case, the formula simplifies to the classic one:

Volume = (4/3) × π × r³

💡 Pro Tip: If your shape is almost spherical, you can estimate the volume using the sphere formula—or make life easier with our Sphere Volume Calculator.

Gauss and the Shape of the Earth

Back in the early 19th century—well before satellites or Google Earth—a German mathematician named Carl Friedrich Gauss asked a bold question: what shape is the Earth, really?

Most assumed it was a perfect sphere. But Gauss had doubts. He suspected Earth was slightly squashed at the poles—what we now call an oblate ellipsoid. Instead of just theorizing, he went out into the field: climbing mountains, hauling gear, and developing new ways to measure long distances with remarkable accuracy.

His pioneering efforts helped establish geodesy, the science of Earth’s shape and size. And he was right: Earth isn’t perfectly round. It bulges at the equator and flattens at the poles—details that matter hugely when designing satellite systems or calculating precise global coordinates.

Fun Facts About Ellipsoids

• The Earth isn’t a perfect sphere—it’s an oblate ellipsoid, meaning it's a bit wider at the equator. The difference is only a few millimeters on scale, but it matters for GPS and space navigation.
• Eggs are natural near-ellipsoids. While not perfect, chicken eggs resemble ellipsoids closely enough that scientists use ellipsoid formulas to estimate their volume in agricultural research.
• Many space rocks and moons are ellipsoid-shaped, not spherical. That’s because their gravity isn’t strong enough to mold them into perfect spheres.
• Medical imaging uses ellipsoids, too. MRI and ultrasound techniques often estimate the volume of organs using ellipsoid approximations—it’s an efficient way to get useful measurements without needing full 3D scans.

You’ll find this and dozens of other helpful calculators in the full Math Tools library, designed for students, educators, and professionals.