If you're here for a quick way to calculate the area of a quadrilateral, our Quadrilateral Area Calculator has you covered. But if you're also curious about how it works—and why quadrilaterals matter far beyond homework problems—this guide is your deeper dive into one of geometry’s most practical heroes.
What Is a Quadrilateral?
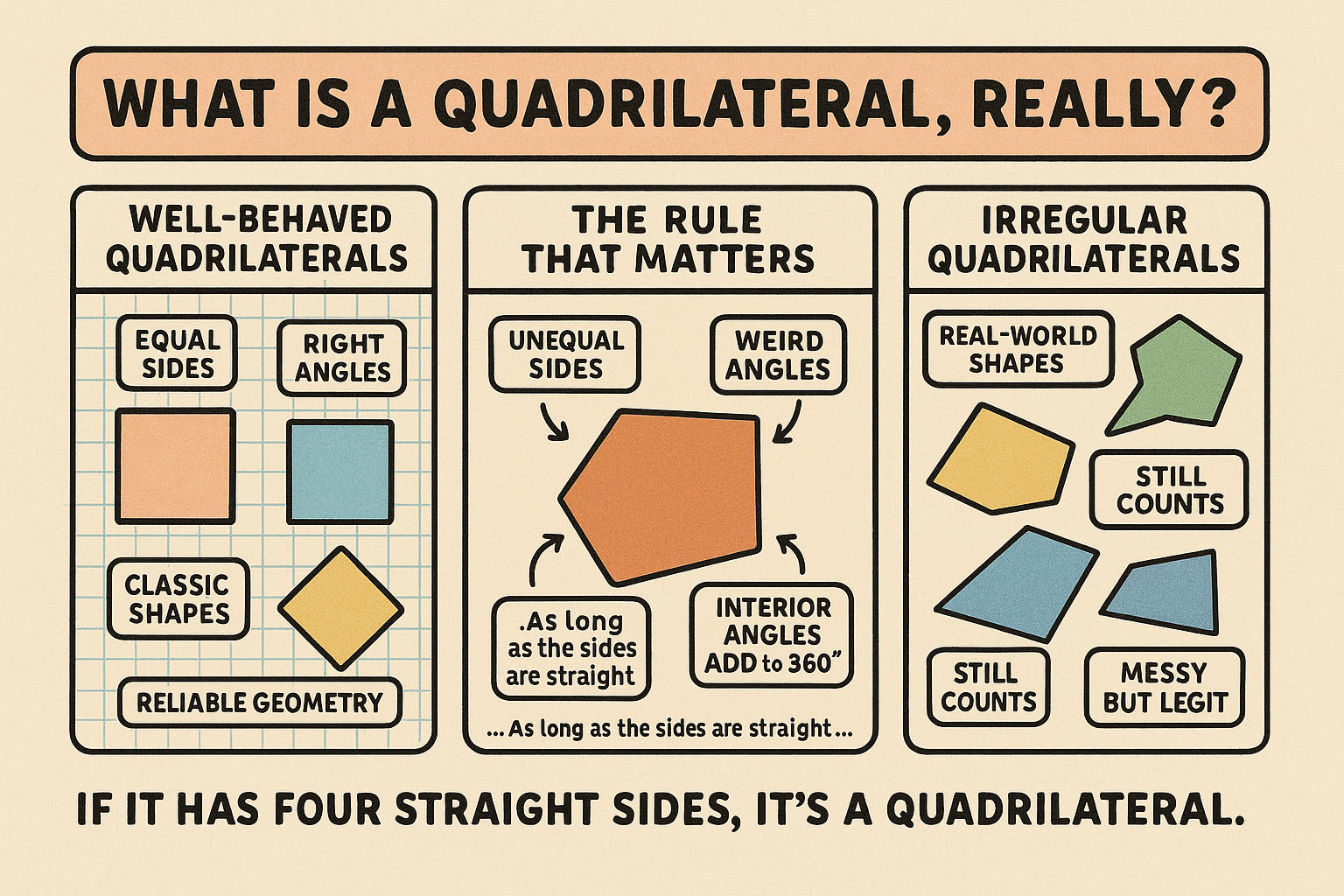
A quadrilateral is a two-dimensional shape with four sides, four angles, and four vertices (corners). It’s one of the most fundamental figures in geometry, and chances are, you encounter quadrilaterals every day—think picture frames, tablet screens, books, and even street signs.
What makes quadrilaterals interesting is how versatile they are. The sides can be equal or different in length, the angles can vary, and some or none of the sides might be parallel. This flexibility gives rise to several well-known types of quadrilaterals: squares (all sides and angles equal), rectangles (equal angles, opposite sides equal), trapezoids (only one pair of parallel sides), and rhombuses (equal sides, but slanted).
Despite their differences, all quadrilaterals share one key property: the sum of their interior angles is always 360 degrees. That rule holds true whether the shape is neat and regular or skewed and irregular.
From math class to architectural design, understanding quadrilaterals is essential for anyone working with shapes, measurements, or spatial reasoning. They’re simple—but powerful—building blocks of both geometry and real-world design.
For four-sided shapes with parallel opposite sides, the Parallelogram Square Footage Calculator makes quick work of the math. You’ll find this tool and many others inside the Math Tools section—perfect for students, teachers, and DIY planners.
How to Calculate the Area of a Quadrilateral
Calculating the area of a quadrilateral depends on the type of shape you’re working with—regular or irregular.
1. Regular Quadrilaterals
If the shape is clean-cut—like a square, rectangle, or parallelogram—use these standard formulas:
-
Square:
Area = side × side -
Rectangle:
Area = length × width
In the case of a parallelogram, the formula becomes:
-
Parallelogram:
Area = base × height
These are foundational in geometry and endorsed in educational standards like those from Khan Academy and the U.S. Department of Education.
2. Irregular Quadrilaterals
When the shape doesn’t fall into a neat category—such as a quadrilateral with all unequal sides—you’ll need a more advanced approach. One of the most effective methods is Brahmagupta’s Formula, which is used when all four sides and one diagonal or the angle between diagonals are known.
Brahmagupta’s Formula:
If you know the lengths of all four sides (a, b, c, d) and the measure of one diagonal (or an angle), you can calculate the area using a more complex variation of trigonometric methods.
For cyclic quadrilaterals (where all corners lie on a circle):Area = √[(s-a)(s-b)(s-c)(s-d)]
where s = semi-perimeter = (a + b + c + d) / 2
For non-cyclic ones, you may need trigonometry or coordinate geometry, especially if working with angles or GPS coordinates.
These advanced methods are essential for professionals working with irregular lots, complex blueprints, or mechanical designs.

How a Kansas Farmer Saved $1,200 With Geometry
Here’s a true story that shows just how useful geometry can be, outside the classroom.
Jack, a farmer in Kansas, was planning to put new fencing around several oddly shaped plots of land. These weren’t neat rectangles—they were irregular, four-sided shapes, the kind you'd never see in a textbook.
Not wanting to waste money, Jack tried to figure out the area of each plot to estimate how much fencing he’d need. But the shapes were too weird, and the math was giving him a headache.
Enter Liam—Jack’s college freshman son, fresh off his first semester of geometry. Liam pulled out a notebook and said, “Let’s try Brahmagupta’s formula. You’ve already got the side lengths and diagonals, Dad.”
With a few quick calculations, they figured out the exact area of each plot. Turned out, Jack had been planning for way more fencing than necessary.
The result? They saved over $1,200—all thanks to knowing how to properly calculate the area of a quadrilateral.
“That formula wasn’t just school stuff,” Jack said. “It paid for my tractor’s new tires".
Fun Facts You Probably Didn’t Know About Quadrilaterals
Let’s lighten things up with a few fun and surprising facts about quadrilaterals—you might start seeing them everywhere after this.
- Your phone screen? Yep, it’s a quadrilateral. Most digital screens—from laptops to smartphones—are rectangles, a type of quadrilateral. Every scroll and swipe happens inside one.
- The Great Pyramid’s Base Is a Quadrilateral. That massive structure in Giza? Its foundation is a nearly perfect square. Ancient Egyptians were using precise geometry thousands of years ago.
- Quadrilaterals Don’t Have to Be Pretty to Be Precise Even if the sides are jagged and angles off-kilter, as long as you have the right measurements, you can accurately calculate the area. No symmetry required.
So whether you’re holding your phone, admiring ancient wonders, or drawing odd shapes in math class, quadrilaterals are quietly everywhere.

Check out Math section to solve math quickly and easily

