Whether you’re solving a geometry problem, crafting a school project, or exploring shapes in design, knowing how to calculate the area of a kite can be surprisingly useful. This elegant, diamond-shaped figure appears in everything from traditional paper kites to architectural patterns and even nature itself. But how do you find its area without getting tangled in complex math? That’s where our Kite Area Calculator steps in. In this guide, you’ll learn what defines a kite in geometric terms, how its area formula works, and where this shape shows up in the real world
What Is a Kite in Geometry?
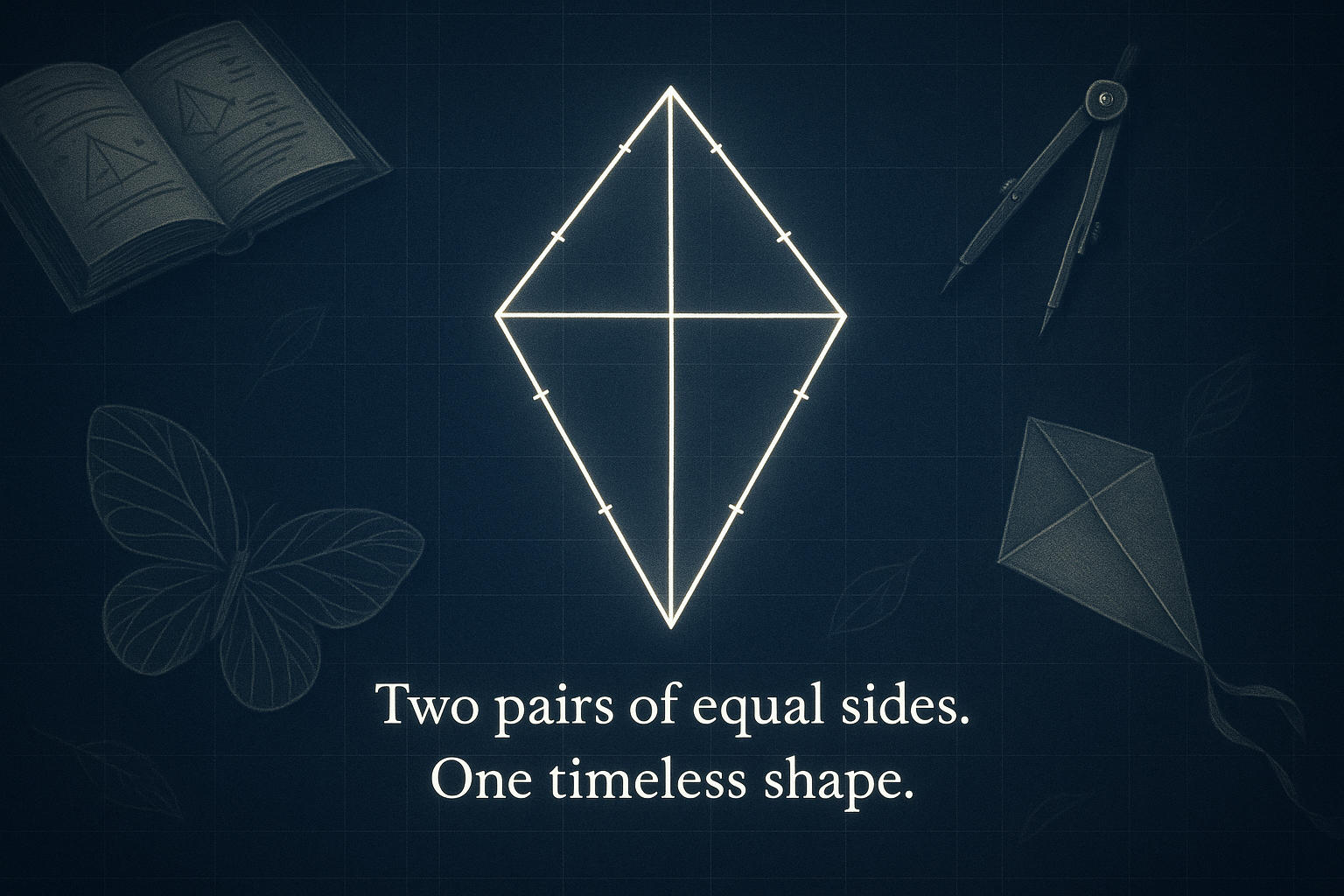
Before we dive into the math, let’s get clear on what we’re actually working with. In geometry, a kite is a four-sided figure — or quadrilateral — with two distinct pairs of adjacent sides that are equal in length. That’s different from something like a rectangle or parallelogram, where the equal sides are opposite each other.
Think of a traditional paper kite — the kind you might fly on a breezy day. Its two top edges are the same length, and its two bottom edges are the same, creating that familiar diamond-like shape. That’s essentially what a geometric kite looks like, too. Not working with a kite shape? The Area Calculator has options for all sorts of 2D figures—basic and complex alike. For more tools that take the stress out of geometry, head over to the Math Tools section and explore the full collection.

How to Calculate Kite Area?
Unlike other shapes that rely on base and height, a kite’s area is calculated using its diagonals. These are the lines connecting opposite corners.
Kite Area Formula:
Area = (d₁ × d₂) ÷ 2
Where:
-
d₁ is the length of the longer diagonal
-
d₂ is the length of the shorter diagonal
Example Calculation:
Let’s say you’re measuring a decorative kite:
-
Diagonal 1 = 20 cm
-
Diagonal 2 = 12 cm
Plug it into the formula:Area = (20 × 12) ÷ 2 = 240 ÷ 2 = 120 cm²
Done! You now know your kite covers 120 square centimeters of space.
Need to convert inches to centimeters first? Use our handy Length Converter to keep your units consistent.
Working with a shape that leans like a kite but has parallel sides? The Parallelogram Square Footage Calculator will give you the right numbers.
Do you know?
Kites may look simple, but they’ve played important roles in history, science, and design. Here are a few facts that might surprise you:
- Kites Are Over 2,000 Years Old
The earliest recorded kites date back to ancient China around 500 BCE. Originally made of bamboo and silk, they were used for military tactics, such as signaling and measuring distances. Legend says General Han Xin once used a kite to estimate tunnel length during a battle strategy.
- Geometrically Symmetrical, Yet Unique
In math, a kite has symmetry along its main diagonal. This line divides it into two equal triangles. However, because not all angles and sides are equal, it’s not a regular shape—making it both balanced and unpredictable.
- Common in Art, Architecture, and Nature
You’ll spot kite shapes in stained glass, floor tiles, and bridge structures. The kite form is visually striking and structurally strong. Even in nature, things like leaf patterns and insect wings often follow this symmetry.