Triangle Square Footage Calculator

If you’ve ever had to measure the triangular corner of a room, design a sloped backyard patio, or outline an oddly shaped plot of land, you’re not alone. Triangles might seem like just another shape from math class, but they’re incredibly useful in real-life situations. From home renovations to outdoor landscaping, knowing how to calculate triangle square footage is a simple yet essential skill that can help save time, money, and effort.

Want to learn more about other shapes? Try our full collection of Square Footage Calculators.

What Is Triangle Square Footage?

Triangle square footage simply refers to how much surface area a triangle covers, measured in square feet (ft²). This measurement comes in handy for a wide range of real-world situations—whether you’re outlining a garden bed, estimating roofing space, or planning how much material to buy for a project. From backyard nooks to irregular floor plans, knowing how to calculate the area of a triangle can save time and help avoid costly mistakes.

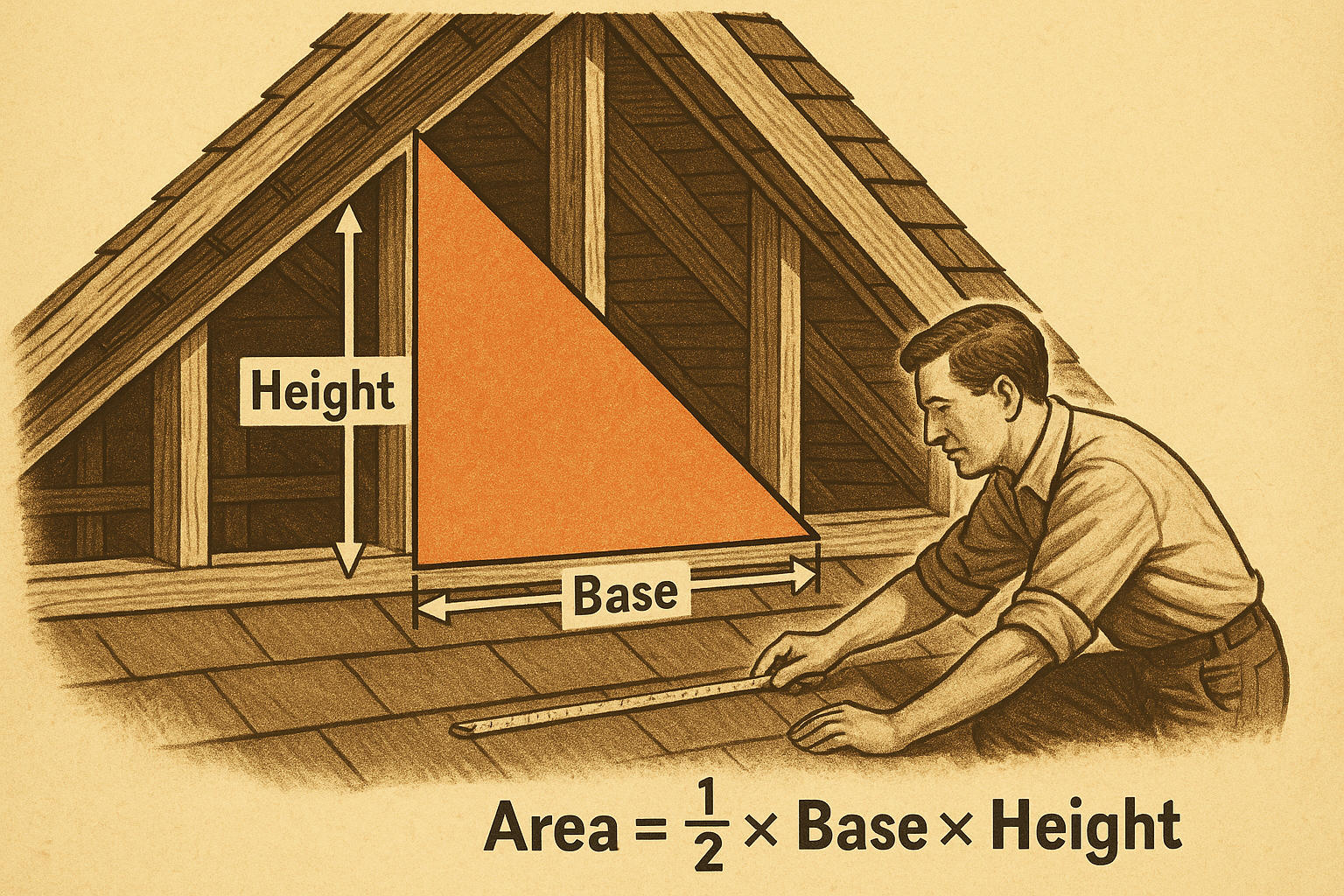
At its core, a triangle is a three-sided polygon with three angles. To find its area, you use a classic formula: multiply the base by the height, then divide the result by two. While it might sound a bit technical at first, the formula becomes second nature once you understand the two key elements—base and height—and how they relate to the shape.

Try out Pentagon Area Calculator

How to Calculate Triangle Square Footage

Calculating the square footage of a triangle is easier than it might appear. With just a few clear steps, you can confidently determine the area of any triangle—whether you're working on a DIY home project, designing a garden layout, or painting a triangular mural.

Step 1: Identify the Base and Height of the Triangle

• The base is usually the bottom side of the triangle, but you can choose any side to serve as the base.

• The height is the perpendicular distance from the base to the opposite point (known as the apex or top).

Step 2: Plug the Values into the Formula

Use the standard triangle area formula:

Area = ½ × Base × Height

This simple formula applies to all triangle types—whether it's equilateral, isosceles, or scalene.

Step 3: Perform the Calculation and Express the Result in Square Feet

Once you’ve inserted your values into the formula, multiply and divide accordingly.

For example, If the base is 10 feet and the height is 6 feet, the math looks like this:
Area = ½ × 10 × 6 = 30 square feet

This method ensures you calculate the triangle’s area in square feet quickly and accurately—ideal for both professionals and casual DIYers.

Try out Regular Polygon Area Calculator

Variations in Triangle Shapes

Not all triangles are exactly the same, and recognizing the different types of triangles can help when determining their area. Although the formula for calculating triangle square footage remains consistent, understanding each shape’s characteristics can make solving geometry problems easier and lead to better interpretation of your results.

Equilateral Triangles

An equilateral triangle features three equal sides and three equal angles—each precisely 60 degrees. While you can still use the standard area formula, you're often provided with just one side length (since all sides are the same). In these cases, a special formula is used to first calculate the height from the side length, which you can then plug into the usual area calculation.

Isosceles Triangles

An isosceles triangle has two sides of equal length and two identical base angles. To find the area, draw a perpendicular from the apex (the point opposite the base) to the midpoint of the base—this gives you the height. Once you have that, it’s easy to apply the familiar formula to determine the square footage.

Scalene Triangles

A scalene triangle has no equal sides or angles, which can make area calculations a bit trickier, especially if the height isn’t provided. If you know all three sides, you might use Heron’s formula instead. But once you figure out the height, you can go back to the standard area method like with any other triangle.

Fun Fact: Geometry in Action

A scalene triangle has three sides of different lengths and no equal angles, which makes the area a little trickier to figure out. If the height isn’t provided, you may need additional details—like all three side lengths—or apply a method such as Heron’s formula. Once the height is known, however, the regular area formula works just as effectively.