Hex Calculator

Curious how hexadecimal magic powers your code, colors, and circuits? This article reveals everything about this number system and its calculators, backed by trusted sources and real‑world tales.

The Building Blocks of Hexadecimals

Let’s start with the basics: hexadecimal is a base‑16 numeral system. It uses sixteen symbols—0 to 9 for values zero through nine, and A to F to represent ten through fifteen. Each of these digits neatly corresponds to four binary digits (bits), which makes the hex system a friendly middleman between human understanding and machine logic1.

Unlike the base‑10 system we use in everyday counting, base‑16 helps us talk directly to computers. A single hexadecimal digit stands in for four binary bits. That means two hex digits already make up a full byte—just the right size to represent values like character codes, colors, or even low-level memory locations.

Ever seen 0x7FFF1234 in a crash log? That 0x prefix flags a hexadecimal number—widely used in memory allocation and IP management. For those working with network infrastructure, IP Subnet Calculator can help bridge the gap between hex-based CIDR ranges and usable host blocks.

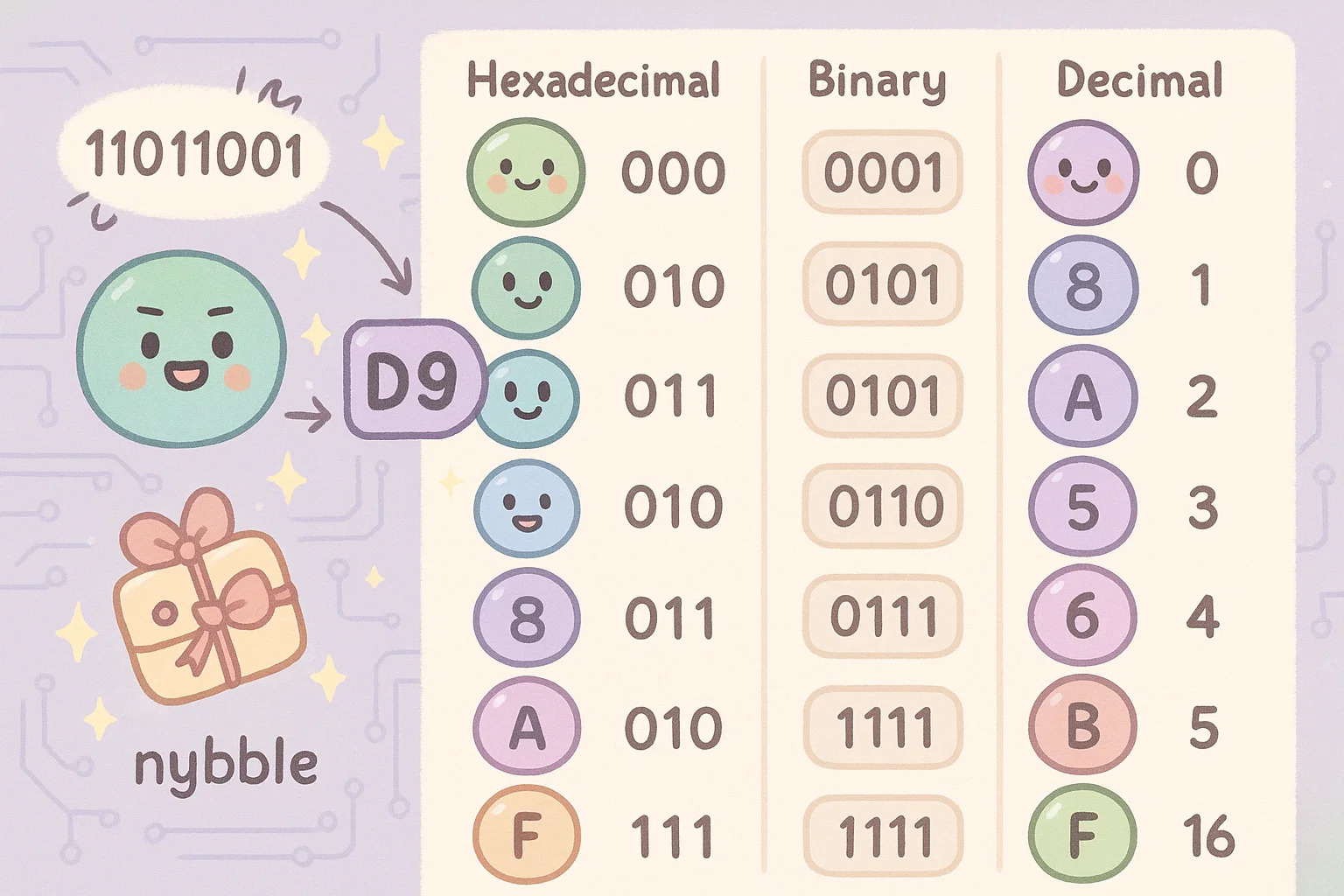
To give a simple visual:

• 0000 = 0

• 1001 = 9

• 1111 = F

This predictable mapping is why hexadecimal appears so often in software debugging, machine-level programming, and networking diagnostics. It reduces long streams of binary into something humans can actually read and interpret without wanting to scream.

You might come across the word "nybble" (yes, it’s a nerdy pun on “nibble”)—this refers to four bits, or half of a byte. One nybble maps exactly to one hexadecimal digit. So instead of writing 11011001, which your eyes will hate, you can simply say D9. It compresses data in a way that's clean, compact, and readable2

“The beauty of hexadecimal isn’t just its compactness. It's about making raw binary digestible—for machines and humans alike.”
— From NASA's binary coding toolkit for student learning³

In technical environments, especially embedded systems and microcontrollers, hex numbers are used because they minimize space while retaining the structure of binary operations. And unlike decimal, which awkwardly slices through binary chunks, hexadecimal respects the binary boundaries computers are built on⁴

Where You’ve Already Seen Hex Without Noticing

You don’t need to be a programmer to have encountered hexadecimal numbers—they’re quietly woven into the fabric of your digital life.

One of the most visible uses of hex is in web design, where color codes are defined using six-digit hexadecimal values. For example, #FF5733 breaks into three parts:

• FF for red

• 57 for green

• 33 for blue

Each pair represents a value from 0 to 255 in decimal—so hex offers a neat, compact way to define millions of color combinations with just six characters. That fiery orange on your favorite website? It’s probably a hex string under the hood^5.

Another space where hex shows up is memory addressing. If you’ve ever peeked into a crash log or read a system error message, you may have noticed something like 0x7FFF1234. That 0x prefix signals a hexadecimal number—commonly used to pinpoint exact locations in your computer’s memory. It's not just a convention; it's a practical shorthand that’s been part of system design since the earliest digital machines⁶

And then there’s the browser bar. Ever seen %20 in a URL? That’s hexadecimal URL encoding at work. Spaces and special characters in web addresses are translated into hex values so they can safely pass through internet protocols.

• For example, "Hello World" becomes Hello%20World

• %20 = ASCII space = binary 00100000 = hex 20⁷

“In ASCII encoding, every character maps to a unique hex value—so URLs, emails, and even passwords often depend on hex translation behind the scenes.” — Federal Networking Council Archives⁸

Even file formats like JPEG, PDF, and ZIP rely on hex markers (called magic numbers) to define their structure. These identifiers, like FFD8 for JPEG or 504B for ZIP, help programs recognize and open files properly.

So, whether you're browsing, designing, or just reading your system's error report, hexadecimal is right there with you—quietly doing its job in the background.

Breaking Down the Math Behind the Code

Hexadecimal math might seem intimidating at first glance, but it’s surprisingly elegant once you get used to its rhythm. At its core, converting hex values into other number systems—like decimal or binary—is just a matter of powers and place value, no different than how we learned base‑10 in school.

Take the hex number 2A. To convert it to decimal:

2A₁₆ = (2 × 16¹) + (A × 16⁰)

      = (2 × 16) + (10 × 1)

      = 32 + 10

      = 42₁₀

The character A here represents the decimal value 10—remember, hex digits go from 0 to F, where F is 15. If you’re dealing with larger values like 2AF, you’d just expand to include 16²:

2AF₁₆ = (2 × 16²) + (A × 16¹) + (F × 16⁰)

      = (2 × 256) + (10 × 16) + (15 × 1)

      = 512 + 160 + 15

      = 687₁₀

Now if you want to go in the other direction—say from decimal to hex—you divide by 16 and keep track of the remainders. For example, converting 255:

255 ÷ 16 = 15 remainder 15 → F

15 ÷ 16 = 0 remainder 15 → F

→ 255₁₀ = FF₁₆

Same logic applies to binary. Each hex digit maps directly to four binary bits, so 2AF becomes:

2 = 0010

A = 1010

F = 1111

→ 2AF₁₆ = 001010101111₂

No rounding, no guesswork—just clean chunking. That’s why developers love using hex for bit-level operations. You can scan memory or color values without needing a calculator (though tools do speed things up). Need to double-check your binary conversions? Try this simple Binary Calculator that pairs well with hex tools.

“Hexadecimal shines in microprocessor design—conversion happens at the bit level without needing additional instruction cycles.”
— Computer Engineering Handbook, U.S. Naval Postgraduate School⁹

Still, having a mental model of how the powers of 16 stack up (16², 16¹, 16⁰...) gives you a deeper appreciation of why hex is so powerful—and where it hides in the math behind the machine.

If you're working on broader numerical conversions, check out this all-in-one Math Calculator to support everything from algebra to fraction simplification.

Hexadecimal Multiplication Table

A Hexadecimal Multiplication Table contains all the products of hexadecimal digits (0-15), making it easier to perform hex calculations without converting between decimal and hex frequently.

Here’s an abbreviated version of the table:

1. U.S. Department of Commerce, NIST Digital Library of Mathematical Functions.

2. Circuit Digest. "Hexadecimal Number System – Explanation and Conversion".

3. NASA's Deep Space Communications Activity Guide

4. CSOS Subscriber Manual – U.S. DEA

5. Vedantu. "Hexadecimal Number System in Digital Applications."

6. U.S. Department of Energy – Advanced Scientific Computing Advisory Committee.

7. Testbook – Hexadecimal Applications in Networking

8. Federal Networking Council Archive Documentation, NSF, 2000

9. U.S. Naval Postgraduate School, Computer Engineering Curriculum Guide