Cube Root Calculator

The Cube Root Calculator is an essential tool for anyone needing to determine the cube root (or 3rd root) of a positive number. This versatile tool not only simplifies the process of finding cube roots but also allows users to cube numbers with ease. Whether you're solving mathematical problems, identifying perfect cubes, or calculating roots of other degrees, the Cube Root Calculator ensures accuracy and efficiency.
What is the Cube Root of a Number?
The cube root of a number refers to the value that, when multiplied by itself three times, gives you the original number. Mathematically, this is written as: ³√x = y which means that y³ = x
Or alternatively: ³√x = x^(1/3)
Let’s break that down: if you’re asked to find the cube root of 27, you’re looking for a number that satisfies the equation y³ = 27. The answer is 3, because 3 × 3 × 3 = 27. This concept plays a fundamental role in arithmetic, algebra, and more advanced mathematical studies.
The Geometry Behind Cube Roots
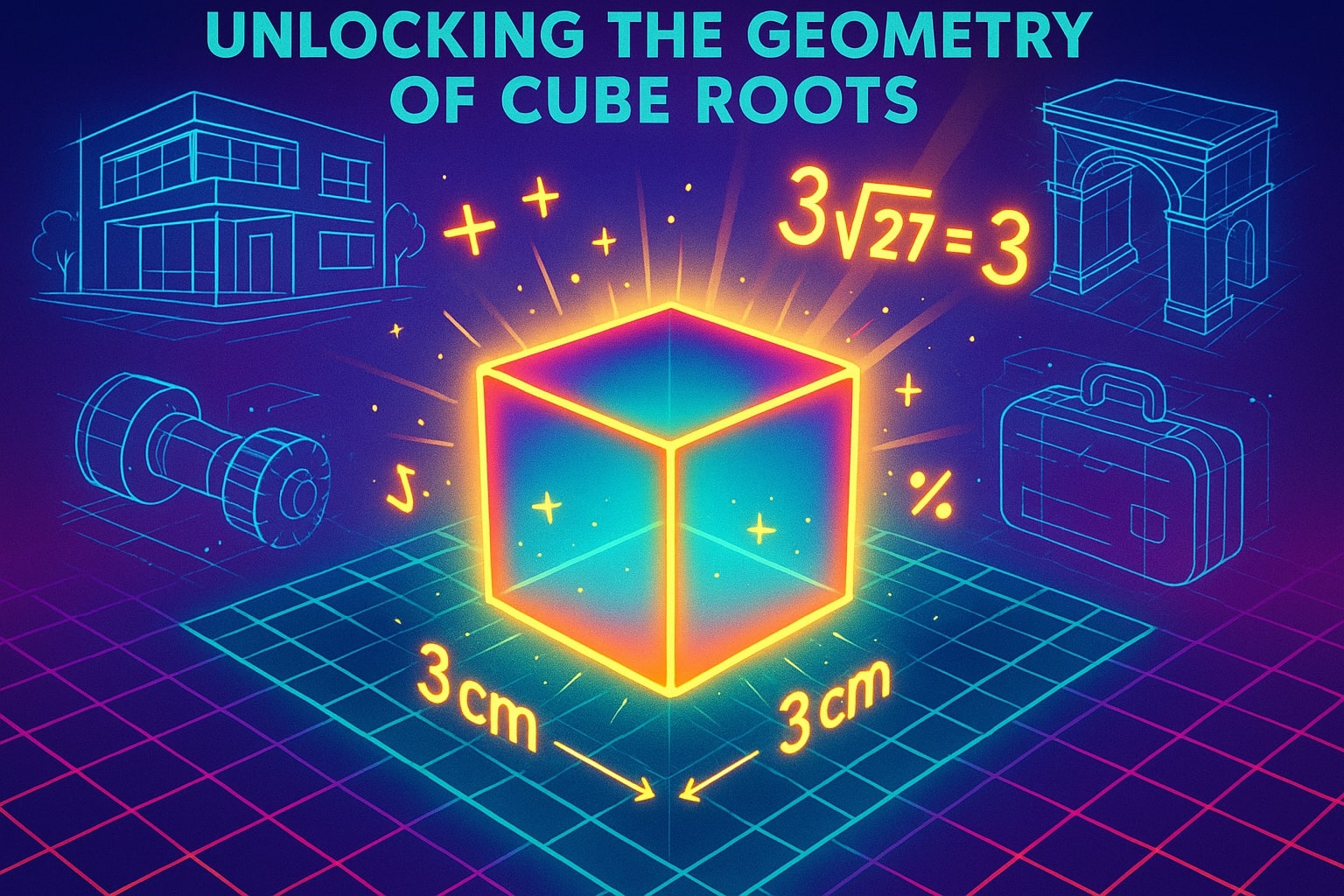
There’s also a spatial interpretation of cube roots. Imagine a cube with a volume of 27 cubic centimeters. To figure out the length of one side, you would calculate the cube root of 27. That gives you an edge length of 3 cm, since 3³ = 27.
This practical connection makes cube roots highly valuable in geometry, engineering, architecture, and product design, where understanding three-dimensional space is crucial.
For related calculations in two-dimensional design, see our Square Area Calculator.
What Are Perfect Cubes?
Perfect cubes are numbers that are the result of cubing whole numbers. Recognizing these values can make solving problems much faster. Here are a few commonly used ones:
These values are often used in geometry, physics, and mathematics for quick reference and problem-solving. Identifying perfect cubes is particularly helpful when working with cube root calculations or determining whether a given number can be expressed as the cube of an integer.
| Number | Perfect Cube |
|---|---|
| 1³ | 1 |
| 2³ | 8 |
| 3³ | 27 |
| 4³ | 64 |
| 5³ | 125 |
| 6³ | 216 |
| 7³ | 343 |
| 8³ | 512 |
| 9³ | 729 |
| 10³ | 1,000 |
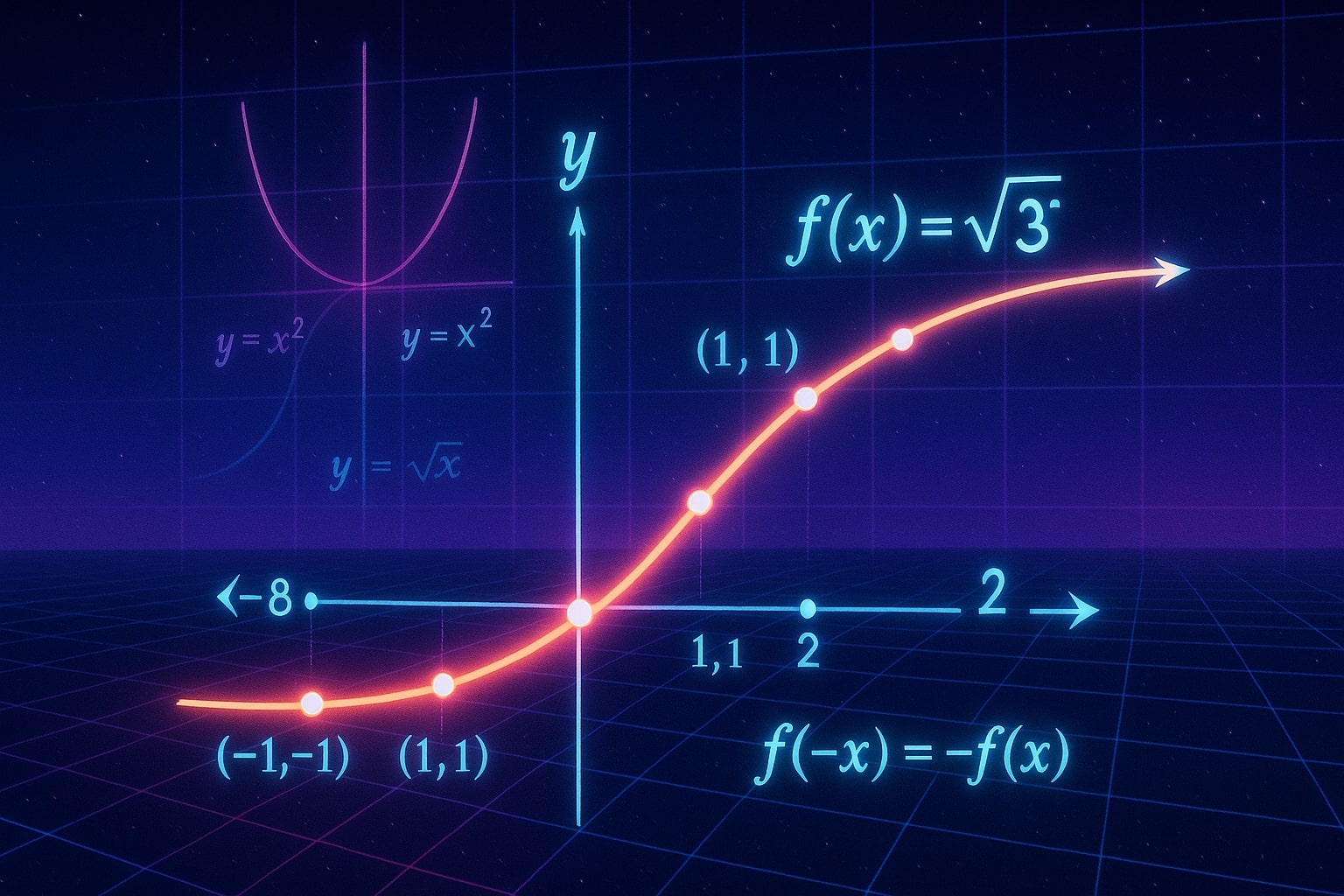
Cube Root Function and Graph
The cube root function, written as f(x) = ³√x, is classified as an odd function, meaning it has rotational symmetry around the origin. This property is expressed as:
f(−x) = −f(x)
Characteristics of the cube root function:
- Passes through the origin: The point (0, 0) is a natural intersection for the graph.
- Domain and Range: Both are all real numbers (ℝ).
- Behavior: As x approaches positive infinity, y also grows. Similarly, as x approaches negative infinity, y becomes smaller.
The graph of ³√x = y demonstrates a gentle curve, gradually increasing or decreasing. This smooth behavior makes it visually distinct from quadratic or square root functions, which have sharper changes in their graphs.
To compare with its two-dimensional counterpart, try our Square Root Calculator.
For more tools like this one, be sure to explore our full suite of Math Calculators
