From planetary orbits to elegant architectural domes, the ellipse area plays a quiet but critical role in how we understand and shape the world around us. You might not calculate it every day, but when you do—whether you're working on a design project, planning landscaping, or diving into a geometry problem. This guide helps you through the ellipse area calculator, shares a practical example from history, and reveals why this oval-shaped figure shows up in everything from athletics to architecture. If you're ready to measure space the elegant way, you're in the right place.
What Is Ellipse Area?
In simple terms, it’s the amount of surface enclosed within an elliptical shape—a kind of elongated circle. Unlike a perfect circle, which has one uniform radius, an ellipse is defined by two axes: one longer and one shorter. These are called the semi-major axis and semi-minor axis, and together, they stretch the shape into its signature curve.
Ellipses aren’t just theoretical—they’re everywhere. In astronomy, they map planetary orbits. In engineering, they guide component shapes and force distribution. And in design, ellipses appear in furniture, mirrors, floor layouts, and even amphitheaters.
From the elliptical tracks runners train on to the layouts of cathedrals, ellipse area helps bring both form and function to the real world.
For other shape types—rectangles, circles, or irregular forms—the Area Calculator brings all your options into one convenient spot. You can explore more calculators like this one in the Math Tools section—designed to simplify geometry, algebra, and real-life measurements.
The Ellipse Area Formula
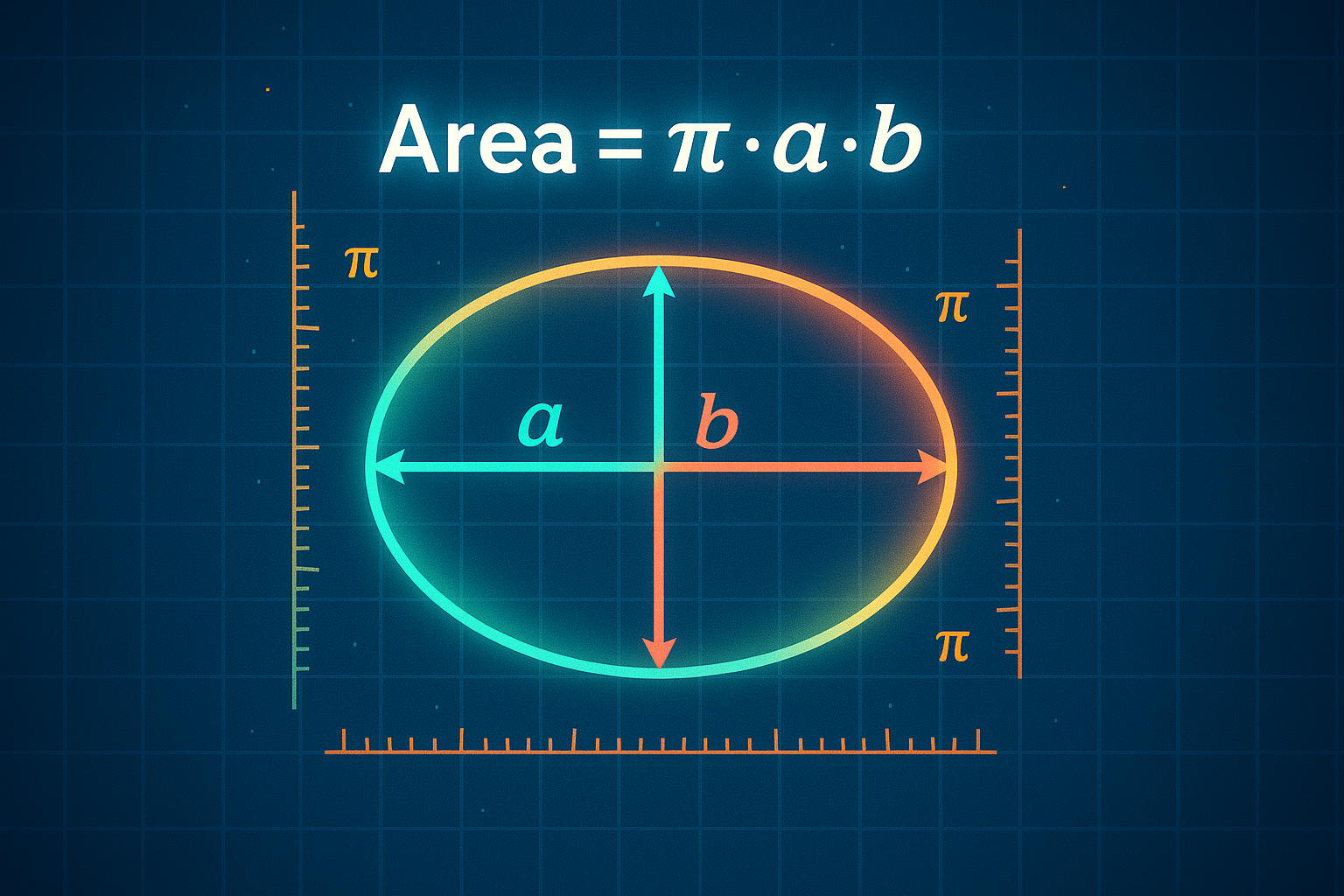
Luckily, calculating the area of an ellipse is much simpler than it may appear. The formula is:
Area = π × a × b
Where:
-
π (pi)is approximately3.14159 -
ais the semi-major axis (half of the ellipse’s longest diameter) -
bis the semi-minor axis (half of the ellipse’s shortest diameter)
Think of it like this: the semi-major axis tells you how wide the ellipse stretches, while the semi-minor axis tells you how tall it stands. Multiply those two values together, then multiply by π, and you’ve got your area—elegant and precise.
If your shape is a perfect circle rather than a stretched oval, the Circle Area Calculator will give you a quick and accurate result.
The Whispering Gallery
One of the most fascinating real-world uses of ellipse geometry can be found not in a textbook, but inside St Paul’s Cathedral in London. Tucked beneath the iconic dome lies a circular passage known as the Whispering Gallery—a place where geometry becomes sound.
Here’s the remarkable part: if two visitors stand on opposite sides of the gallery’s curved wall—over 100 feet apart—one can whisper against the wall, and the other can hear it clearly across the space. No microphones. No echoes. Just perfectly guided sound.
Why does it work? Because of the way ellipses reflect waves. In any ellipse, a sound (or light) wave that begins at one focus point will naturally reflect off the curved wall and travel directly to the other focus. This principle, like the one behind the ellipse area formula, shows how two simple axes can define far more than space. They also shape how sound moves.
This architectural choice was no accident. The designers of St Paul’s harnessed the power of ellipse mathematics to create not just a beautiful structure, but an awe-inspiring experience still enjoyed by visitors centuries later.


